基本概念
- base::不同进制之间的运算
适用范围
- 任意进制之间
- 整数部分
1. 直观理解
1. 实例:
1.1. 之一
用十进制15转二进制1111举例:
- 15/2得到商7余1,即15分成了两部分14和1
- 14是2的倍数,说明14这部分在假设最后得到的二进制数中肯定不在第一位,而是进位到第一位后面的位了。
- 而这个1就是不能够进位的,故得到了第一位二进制数是1
- 而14这部分数都是第二位往后的数值,14除以2就是将第二位往后的数位全部右移,得到的商即7是14右移的结果。
- 取上次的商作被除数 ,7/2得到商3余1,分为了两部分6和1
- 所以右移后的第一位,也就是完整二进制数的第二位,为1
- 再上次的商作被除数 ,3/2得到商1余1,如法炮制,完整二进制数的第三位为1
- 再取上次的商 ,1/2得到商0余1,完整二进制数的第四位为1,同时,商为0说明原二进制数第四位后面就没有数值了
综上所述,得到二进制数1111
1.2. 之一
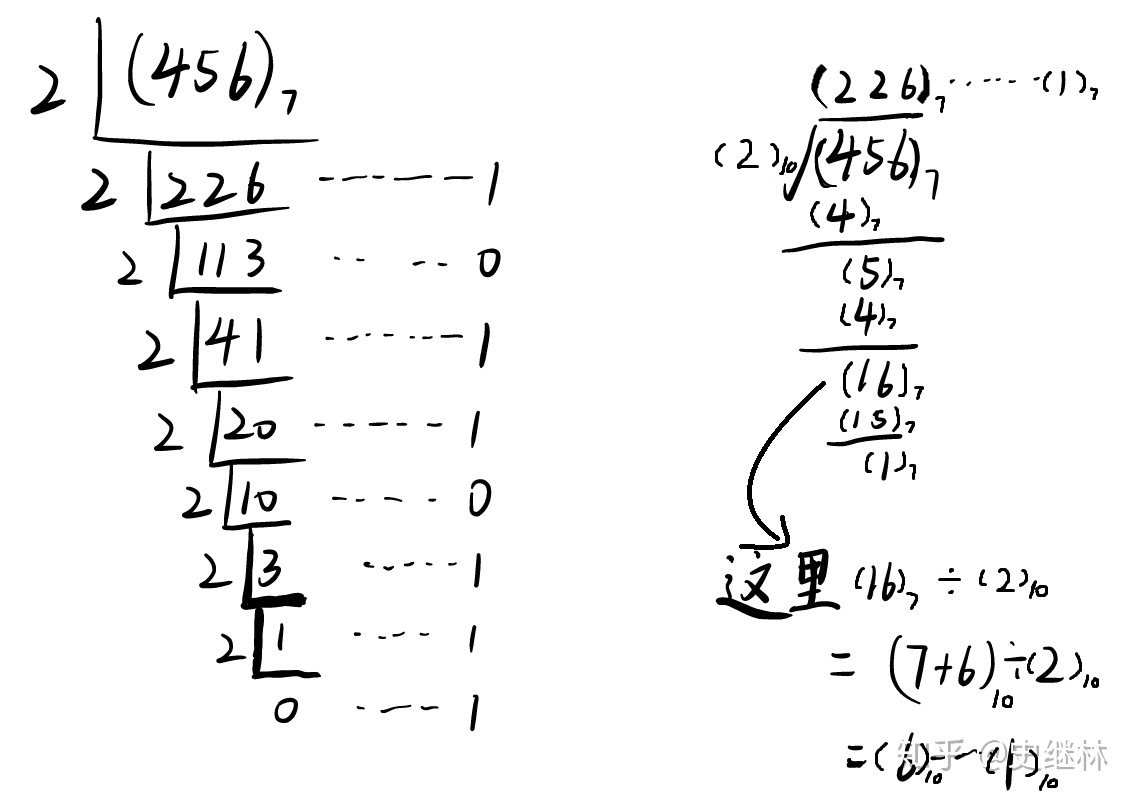
2. 原理:
- 运算对象为假设的转换后的数,用除法分成两部分,一部分是第一位,另一部分是第二位以后的。
- 即可取出第一位。将另一部分右移,对右移后的数再套用上述操作。即可逐位求出假设的数。
2. 方法:
- 假设有转换后数,然后将被转换数除以目标进制数,取余数作为第一位,把商再除以目标进制数,取余数作为第二位…以此循环,以商等于0为出口
father:: 进制转换