高数下 九 6 (2) 空间曲线的切线与法平面

实例:

1. 说明:

1. 目标是把曲线原方程组化为标准的向量值函数
   1. 第一条方程确定了隐函数y=y(x)
   2. 再多加一条方程x=x

1. 空间曲线的切线方程:

1. 求某点的切线方程:

1. 算出该点的一个切向量, 记作T
   1. 对一般方程,方法:
      1. 将曲线方程转换为向量值函数方程
         1. 详见高数下 九 6 (1) 一元向量值函数及其导数
      2. 求向量值函数在这点的一阶导数
      3. 从两个切向量中随便取一个
   2. 对参数方程,方法:
      1. child::直线参数方程的切向量(方向向量)
2. 用对称式求切线方程

2. 空间曲线的法平面:

1. 直观理解：

空间中垂直于切线的法线有很多条，它们共同构成了一个法平面

2. 求某点的法平面:

1. 算出该点的一个切向量
   1. 求向量值函数在这点的一阶导数
   2. 从两个切向量中随便取一个
2. 用点法式求法平面

3. 求空间曲线的切线与法平面的常用题目模型:

1.

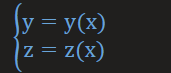
1.1. 解:

1. 
2. 变成了标准的向量值函数, 按部就班即可

2.

1. 解:
   1. 通过方程组的隐函数的确定规则转换为上一种模型
   2. 
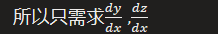
      1. 通过隐函数求导法则