高数下九 4 多元复合函数的偏微分

1. 相关概念:

1.1. x关于x函数的求导为1

1.2. dz于∂f的区别:

对于z=f(x,y) z函数是指换元到最里层的函数 f函数是指没有换元的初代函数

2. 使用旧知识直接求导法(适用于具体函数):

2.1. 梗概:

1. 沿用”求导复合函数”的知识
2. 需要注意:
   1. 清楚谁是因变量
   2. 如果复合函数中没有偏微分的自变量, 就当作常数, 否则一步一步向内求导

2.2. 实例:

1. 
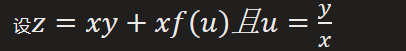
2. 求$\frac{\partial z}{\partial x}$
   1. 把y看作常数
   2. 把f(u)和u看作复合函数
3. 

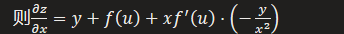
3. 公式法(适用于抽象函数):

3.1. 梗概:

1. 初始函数中所有变量中与x 有关的, 沿着x的路径进行求导
2. 把所有到x的不同路径都求导
3. 如果函数中有多个就偏导, 有一个就普通求导

3.2. 实例:

有函数z=f(x,y,u), u=u(x,y) 则

3.3. 图解: