时间复杂度

算法

梗概

• 有三个变量: 规模N, 输入数据, 算法本身
  • 通常只考虑规模N，即只考虑T(N)
• 主要考虑最坏情况的时间复杂度
• 主要用渐进表达式O(N)代替T(N)
• 程序实际运行次数T (n)=…

1. 公式记法:

T (n) = O (f (n)) 其中n为问题的规模, f (n) 为语句关于n所消耗时间的函数

分析方法

实际判断时间复杂的方法:

1. 常识感觉哪里时间耗费最多
2. 忽略其他时间耗费少的执行次数
3. 用数学知识算出时间耗费最多的地方的执行次数
4. 当实在没办法的时候，可以代数进去找规律
5. 取增长速度最快的n
6. 去掉系数和常数

实例

3. 常见时间复杂度

1. 里层循环与外层循环长度互补

时间复杂度为O(n²)

for(i=0;i<n;++i){
//pass
	for(j=i;j<n;++j){
	//pass
	}
}

2. 循环进度指数增长

之一

时间复杂度为O(logn)

for(i=2;i<n;i=i*2){
  //pass
}

详细推导

• 运行多少次，就乘上多少个2，所以结束时有$n=2\times 2^{T(n)}$
• 所以$T(n)=lo{g}_{2}n-1$
• 因为时间复杂度去掉系数和常数
• 所以O(n)=logn

之一：非常少见

时间复杂度为O(logn)

for(i=2;i<n;i=i*i){
//pass
}

2.1. 详细推导:

1. 执行多少次，就要套多少次平方，即数学关系得$2^{2^{T(n)}}=n$
2. 所以$T(n)=lo{g}_{2}lo{g}_{2}n$
3. 当n极限大的时候，函数导数近似于logn
4. 所以O(n)=logn

递归

原文：12.4   汉诺塔问题 - Hello 算法 如图所示，汉诺塔问题形成一棵高度为 𝑛 的递归树，每个节点代表一个子问题，对应一个开启的 dfs() 函数，因此时间复杂度为 𝑂($2^n$) 。

• 每展开一层递归, 就乘上2 , 所以最终乘上n个2
• $T(n)=2\times (T(n-1))=2\times (2\times (T(n-2)))=...=2^n$
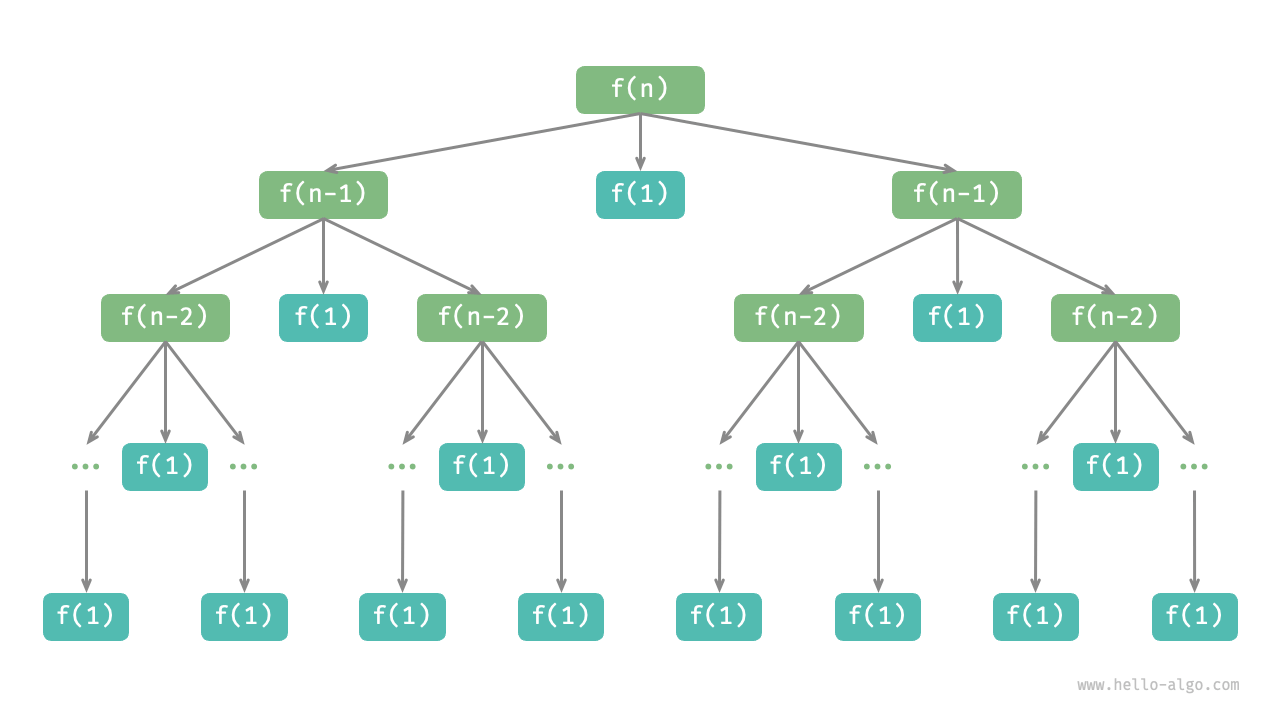
  • 这里忽略了常数T(1)