1. 点积:
1. 几何意义:
将一个向量投影到另一个向量的所在的一维空间中, 然后用投影值乘另一个向量的长度
2. 向量的叉积(向量积):
1. 助记:
- 叉积的顺序很重要
- 叉积用右手螺旋定则确定方向
- 叉积大小与两向量的模与方向都有关, 垂直时最大
2. 叉积的几何意义:
- 叉积的模就是平行四边形的面积(以这两个向量为邻边)
- 叉积的模就是两个向量围起来的三角形面积的两倍
3. 计算叉积:
3.1. 确定叉积方向
用右手螺旋定则: 四指指向第一个向量, 四指往第二个向量方向收拢, 拇指方向即叉乘结果方向
3.2. 叉积结果大小计算公式:
2.3.2.3. 公式三:
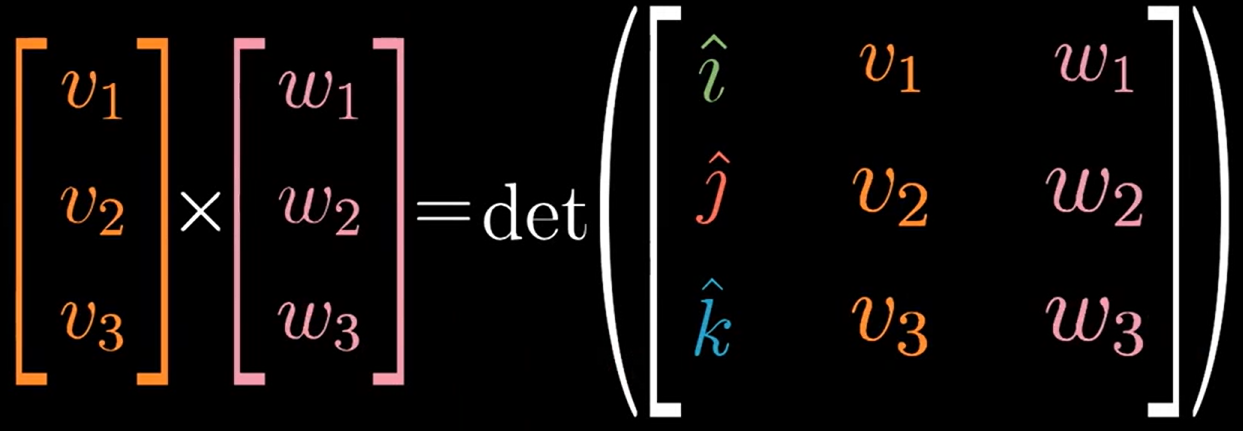
适用范围:
- 含有未知数, 向量是抽象的
- 向量间的几何关系不知道
实例:
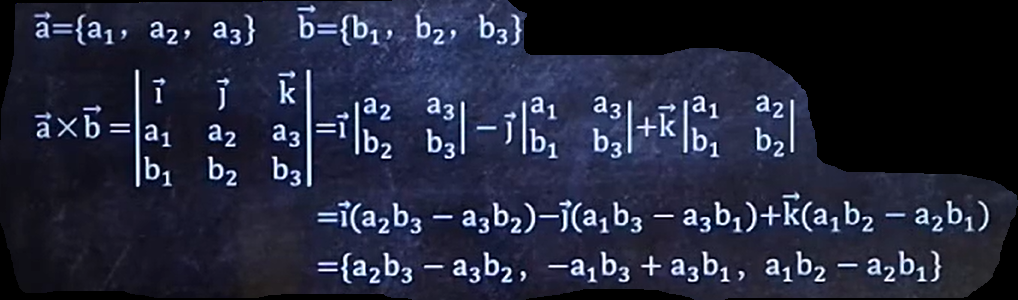
2.3.2.1. 公式一(不方便):
![]()
2.3.2.2. 公式二(推荐,符合直觉):
引入物理概念中的力臂, 记作d 力臂的直观理解: child::
则叉乘大小为Drawing 22-06-09.excalidraw
⚠ Switch to EXCALIDRAW VIEW in the MORE OPTIONS menu of this document. ⚠
Text Elements
a
b
Embedded files
359167bf4209643c0543ba0ee9860a5695b06cb3:
指向原始笔记的链接
适用范围:
- 向量已知, 是具体的
- 向量间的几何关系已知
4. 运算规律:
4.1. 不符合常识的运算规律(以下部分省略向量箭头):
2.4.1.1. 反交换律:
a×b = -b×a。
2.4.1.2. 雅可比恒等式(暂时忽略, 还没学到):
a×(b×c)+b×(c×a)+c×(a×b) = 0。
2.4.1.3. 两个平行向量叉积为0
2.4.1.3.1. 
![]()
2.4.1.4. 求导叉乘:
类似函数相乘
前导×后不导+前不导×后导
(注意保持叉乘顺序)
2.4.1.5. 叉积逆运算:
child::叉乘逆运算
4.2. 符合常识的运算规律:
2.4.2.1. 分配律:
a×(b+c) = a×b+a×c。
2.4.2.2. 与数乘法兼容交换律:
(λa)×b = a×(λb) = λ(a×b)。
2.4.2.3. 数乘结合律:
(λa)×(μb) = (λμ)(a×b)
5. 符号记法:
![]()
6. 特殊性质:
![]()