正项级数

正项级数可以使用三种审敛法:

比较审敛法 ; 比值审敛法 ; 根号审敛法

定义: 每项都为正数的级数

性质:

1. 级数收敛 ⇐> 部分和数列有界(几乎没啥用)

2. 收敛发散的传递性

对两个级数u和v, 存在u的项总是小于v对应项 则大级数收敛<!> 小级数收敛 小级数发散>大级数发散

2.1. 推论: (几乎不用)

从中间某一项开始, u的项小于v对应项×k(k>0), 则大级数收敛<!> 小级数收敛, 小级数发散>大级数发散

比较审敛法

1. 前提: 比较审敛法必须是对正项级数

2. 梗概: 利用收敛发散的传递性, 对原级数进行放缩

3. 通常和三个级数进行比较:

3.1.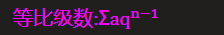

3.2.

3.3.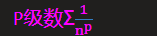

4. 使用该方法需要确定两个问题:

1. 放还是缩, 即>=还是⇐
2. 和谁比

极限改进的比较审敛法:

1.

1.1. 若l=0, 且$v_n$收敛 <!⇒ un收敛

助记: 即un每一项都比收敛级数vn要小, 故un也收敛

1.2. 若0<l<+∞ vn收敛或发散 ⇒ un收敛或发散

助记: 即相当于un=某个常数×vn, 则收敛发散性不变

1.3. 若l=＋∞, vn发散 ⇒ un发散

助记: 即un每一项都比发散级数vn还大, 故un发散

2. 总助记:

l取两个极端的中间时, v_n不管收敛还是发散都能传导给u_n l取0时, 即u_n较小, 只能传导收敛给u_n l取+∞时, 即un较大, 故只能传导发散给un

3. 使用该法需要确定的一个问题:

只需要考虑和谁比, 不用考虑放还是缩

比值审敛法:

1.

1.1. ρ<1 ⇒ 收敛

1.2. ρ>1 ⇒ 发散

1.3. ρ=1时无法判断

2. 助记:

用后/前, 如果后大,即越来越大>发散 如果后小, 即越来越小>收敛

根值审敛法(柯西判别法):

1. 适用范围: 通项与n次方有关

2.

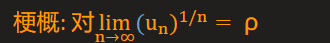
2.1. ρ<1 ⇒ 收敛

2.2. ρ>1 ⇒ 发散

2.3. ρ=1 无法判断

3. 助记: 把un看作n次方, 根号后得到基数

基数小于1, 往0逼近>收敛 基数大于1, 不断变大>发散