实例:
1. 视频讲解:
2. 图片讲解:
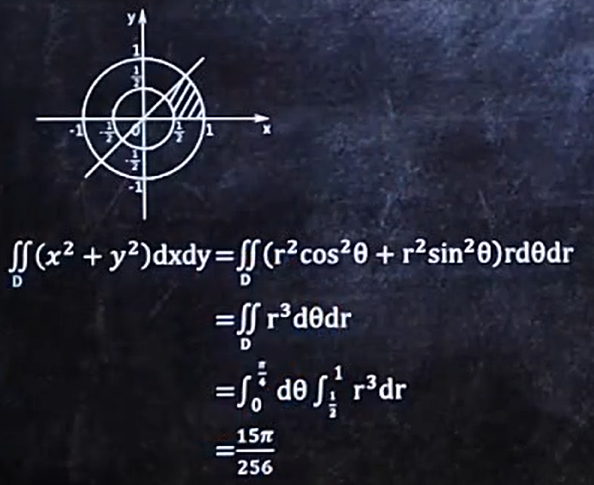
1. 适用范围:
1. 对积分区域:
- 圆
- 圆环
- 扇形
2. 对被积函数:
- f(x²+y²)
- f(x/y)
- f(y/x)
- 其他能消掉ρ或θ的特殊函数形式
2. 梗概:
计算极坐标二重积分即特殊的二重积分换元法 即
- 换元直角坐标二重积分的所有x和y x=ρcosθ y=ρsinθ
- 按极坐标展开单位面积 dσ=ρdθdρ(⭐)
- 里层积长度ρ, 外层积角度θ
3. 详细步骤:
- 画出积分区域
- 把所有的x和y都换元
- 确定角度θ上下限, 作为外层积分
- 确定曲线(以ρ为因变量)上下限, 作为里层积分
- 离原点远的为上限, 近的为下限
4. 注意点:
- 展开单位面积dσ时, 不要漏掉ρ
- 换掉所有的x和y
- 极坐标二重积分只有一种顺序,
- 即外层角度θ, 里层ρ(通常是两条曲线包围)