多元函数的极值与最值及其求法

相关概念:

1. 驻点:

1.1. 定义:

对二元函数:

对更高维函数:

类似的, 对每个坐标分量的偏导=0

极值点可能存在位置:

只可能存在于某些驻点中

求极值点:

1. 对无条件的极值点(无约束条件)

child::

求无约束条件的极值点

0.1. 对显示二元函数:

1. 求$f_x^{\prime }和f_y^{\prime }$

2. 求$f_{xx}"和f_{xy}"和f_{yy}"$

3. 求所有驻点

1. 按驻点定义解出所有的x和y
2. 每个x和每个y都排列一次, 组成驻点

4. 求每个驻点对应的以下三个值

1. 
2. 
3. 

5. 计算AC-B²

对每一点所对应的AC-B², 分情况得出结论:

1. >0 再对A分情况:（助记: 正才有极值) (助记: 都是以x为自变量的二阶偏导数, 很和谐)
   1. A<0 ⇒ 该点为极大值点
      1. (助记: 二阶导数小于零, 和一元函数极值判定一样, 巅峰则落)
   2. A>0 ⇒ 极小值点 2. (助记: 二阶导数大于零, 和一元函数极值判定一样, 谷底则起)
2. <0 没有极值点 (助记: 负没有极值)
3. =0 无法判断 (助记: 剩下的情况不能判断)

6. 实例:

对隐式二元函数:

1. 步骤梗概:

与显式二元函数的步骤绝大部分相同, 只有求驻点哪里有区别

1.1. 求所有驻点:

1. 按以下方程组解出所有的x和y $\{\begin{array}{c}\frac{dz}{dx}=0\\ \frac{dz}{dy}=0\\ 原方程\end{array}$
2. 每个x和每个y都排列一次, 组成驻点

2. 实例:

指向原始笔记的链接

2. 对有约束条件的极值点:

2.1. 化为无条件极值点

1. 用原函数和约束条件联立

2.2. 用拉格朗日乘数法求

1. 对原函数f(x,y); 约束条件1: φ(x,y)=0 ; 约束条件2: v(x,y)

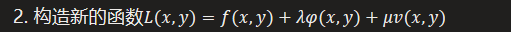
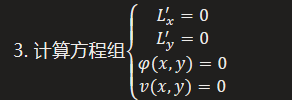
求最值:

1. 对通用问题:

求以下三个点的值(最值点的所有可能位置)

1. 驻点
2. 偏导不存在的
3. 端点

2. 对实际问题:

2.1. 只用求驻点(通常只有一个)

原因: 实际问题最值点很少在端点处或偏导不存在的点