2. 浮点数:
浮点数也是人为规定的一种存储和读取规则
浮点数由三部分组成,即S(符号位)和E(指数位)(阶码)以及M(尾数)。
1. 规格化表示公式:
V = (-1)^S * 1.M * 2^E (该公式不能表示零)
2. 当公式表示二进制数时:
类似于科学计数法,E为正数时,就将1.M的小数点往右移动E位,负数类似处理。
3. 当公式表示十进制数时:
直接计算结果即可。
而现在主流的浮点数规则是IEEE754 浮点数标准
如图为IEEE754的规定
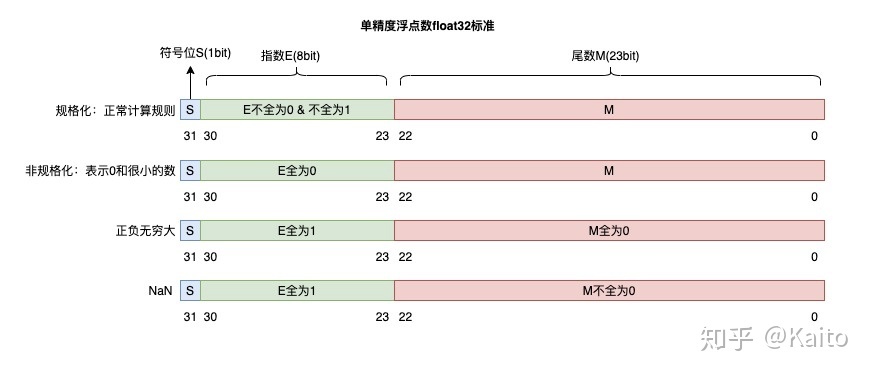
示例
表示十进制0.1
十进制0.1 转换为二进制表示:
-
首先将0.1转换为二进制小数([use::进制转换-小数转换]):
0.1 * 2 = 0.2,整数部分为0
0.2 * 2 = 0.4,整数部分为0
0.4 * 2 = 0.8,整数部分为0
0.8 * 2 = 1.6,整数部分为1
…(继续这个过程直到小数部分足够准确) -
得到二进制表示为:
0.00011001100110011001100110011001100110011001100110011… -
根据IEEE754规范进行标准化表示:
- 符号位S为正号(因为是正数)
- 尾数M是小数点后的所有位,即一直重复的0011…
- 指数E需要将小数点左移动至尾数第一位前的位置,这里是第4位,所以E=4+127=131(127是一个偏置值)
因此,十进制0.1在IEEE754浮点数标准下的表示为:
- S: 0
- E: 131 (用8位二进制表示为10000011)
- M: 尾数中的有效数字(即110011001100110011001101…去掉尾数中故有的0)
所以该浮点数可以表示为:0 | 10000011 | 10011001100110011001101
这就是十进制0.1在IEEE754浮点数标准下的二进制表示。
3. IEEE754标准详解:
1. 一、IEEE754 浮点数标准对位数的规定:
1.1. 这个标准统一了浮点数的表示形式,并提供了 2 种浮点格式:
-
单精度浮点数 float:32 位,符号位 S 占 1 bit,指数 E 占 8 bit,尾数 M 占 23 bit
-
双精度浮点数 double:64 位,符号位 S 占 1 bit,指数 E 占 11 bit,尾数 M 占 52 bit
2. 二、IEEE754 浮点数标准对指数和尾数的规范化:
2.1. 为了使其表示的数字范围、精度最大化,浮点数标准还对指数和尾数进行了规定:
尾数 M 的第一位总是 1,因此这个 1 可以省略不写,它是个隐藏位,这样尾数就可以多一位拿来表示。
- 由于各种原因,E不用补码表示,所以为了使 E 的取值范围为 -127 ~ 128,我们规定将E再减去127。而double也作类似处理。
3. 三、IEEE754 浮点数标准对其他情况的规定:
3.1. 除了规定尾数和指数位,还做了以下规定⭐:
child::特殊浮点数的表示
4. 四、IEEE754标准总共列出了4 种不同的舍入方法:
- child::浮点数的舍入
5. 浮点数加法法则:
先把小的E对齐大的E(阶码),再相加
而对齐E是:将E对齐,然后将M(尾数)右移两个E相差的绝对值(右移运算就是除2,也就是将小数点向右移动)
[use::短除法 整数进制转换]
father:: 计算机组成原理