1. 常规筛
- 1.输入一个n,求1-n之间的素数,那么肯定要有一个循环将1到n都过一遍。
- 2.判定素数,除了1和它本身外没有其它的因数,所以,这里也要有一层循环,将2-n-1之间的数都判断一遍。
- 3.根据题目要求输出。
1. 优化点:
- 1.首先要有一个标志位flag,事先标记为1,说明这个j是素数,在第二层循环中,只要有j可以被整除,那么就将其标记为0,退出第一层循环,紧解输出。`
- 2.通常萌新们在第二层循环的条件部分写i<n,这样时间复杂度为O(n^2),不太好。
- 3.再优化一下,i⇐j/2;聪明一点的萌新会发现,我只要判断到j的一半就行了,因为小于j一半的因数的个数和大于j一半的因数的个数是相等,也就是以j的一半为界成对出现。 这样时间复杂度就为O(n^2/2),好像还行,但阶数没有降下来。数据规模很大的话1/2就没有意义了。`
- 4.再优化一下,i * i⇐j;或者i⇐sqrt (j) 其实已经有数学给出了证明,j的因数是以j的方根对半分布的,也就是说,小于j的方根的因数的个数和大于j方根的因数的个数是相等。这样时间复杂度就为O (nsqrt (n)) ,这样的话已经不错了,足够解决大部分的相关问题了.
补充:(一,首先脑子要有一个基本的模型解法或者基本思路,学习的话就根据前辈的思路走,不要直接看代码,先实操;二,建议从网上多阅读一些有关时间复杂度的资料,这样可以逐步建立代码优化的方向,空间复杂度和代码复杂度就略过了,不太重要。三,其实还有其它的优化方法来提高运行速度,优化思路增加约束(去除很明显不必或重复计算的))
2. 埃氏筛
1. 基本思路:
- 首先,2是公认最小的质数,所以,先把所有2的倍数去掉;然后剩下的那些大于2的数里面,最小的是3,所以3也是质数;然后把所有3的倍数都去掉,剩下的那些大于3的数里面,最小的是5,所以5也是质数…
- 上述过程不断重复,就可以把某个范围内的合数全都除去(就像被筛子筛掉一样),剩下的就是质数了。
- 复杂度为O (nlogn)
2. 图解:
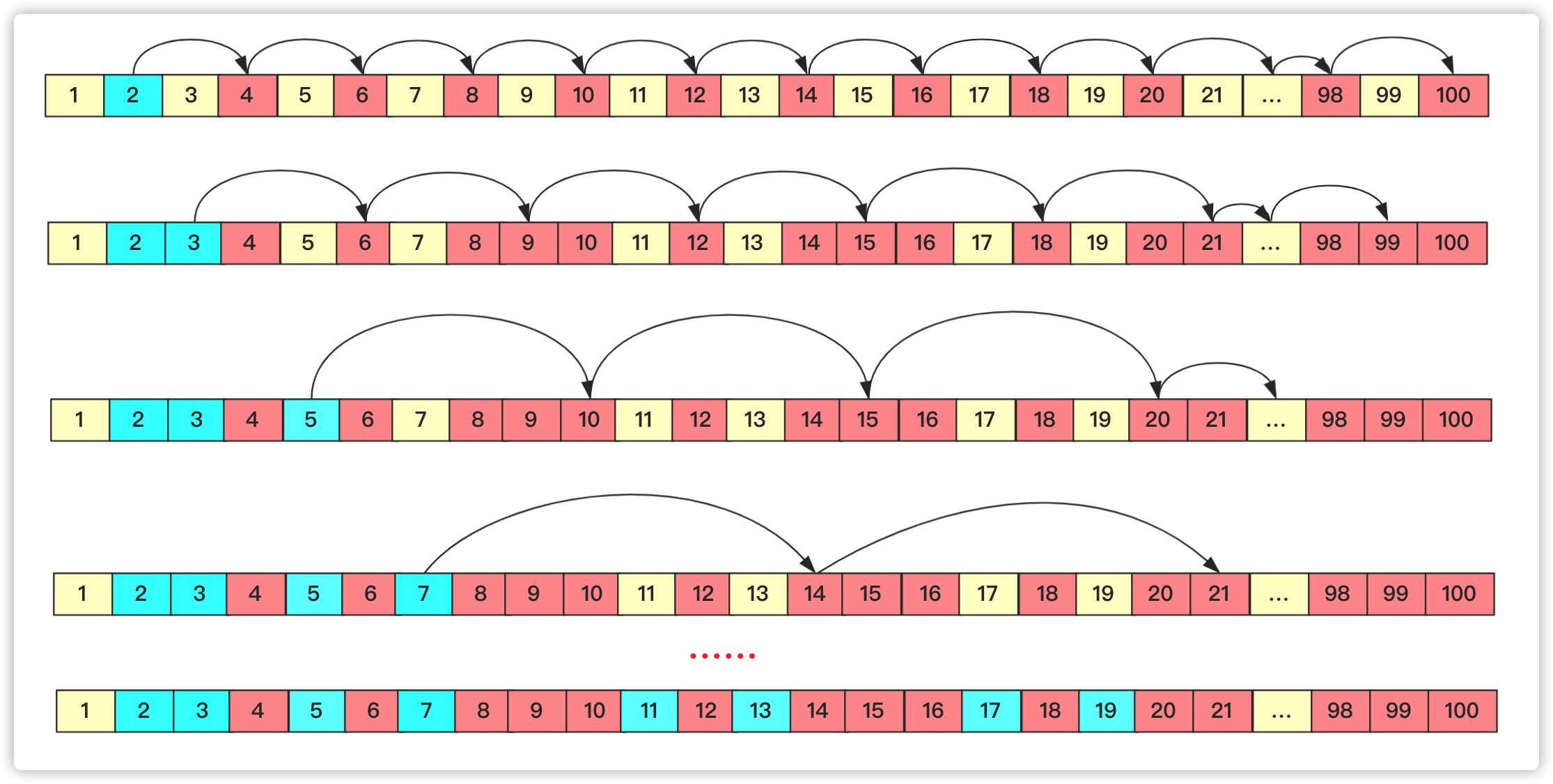
3. 代码:
long long max=200000;
long long a[max],i,j;//可以计算到max
long long n;
cin>>n;
a[0]=0;
for(i=1;i<=n;i++)
a[i]=i;//赋对应值
a[1]=0;
for(i=2;i<=n;i++){
if(a[i]==0)//被标记为零不是质数,
continue;//跳过下面代码部分,直接进入下一次循环
cout<<i<<endl;//筛出来的就是质数 输出
for(j=i;i*j<=n&&j<n;++j)//就是上面写的基本思路
a[i*j]=0;
}
return 0;3. 欧拉筛
- 线性筛,复杂度为O(n)。与埃氏筛相比,不会对已经被标记过的合数再进行重复标记,故效率更高。欧拉筛将合数分解为 (最小质因数 * 一个合数) 的形式,通过最小质因数来判断当前合数是否已经被标记过。
const int maxn = 10000; // 表长
int prime[maxn], pNum = 0; // prime记录素数,pNum记录素数个数
bool p[maxn] = {false}; // p记录当前数是否被筛去
void eulerSieve(int n) {// 查找记录2-n的素数{
for (int i = 2; i <= n; i++){
if (p[i] == false) // 如果未被筛过,则为素数
prime[pNum++] = i;
for (int j = 0; j < pNum; j++){
if (i * prime[j] > n) // 当要标记的合数超出范围时跳出
break;
p[i * prime[j]] = true; // 将已经记录的素数的倍数进行标记
if (i % prime[j] == 0) //关键步骤,用于避免重复标记
break;
}
}
}欧拉筛的难点就在于对 if (i % prime[j] == 0) 这步的理解,当 i 是 prime[j] 的整数倍时,记 m (某个整数) = i / prime[j]
那么 i * prime[j+1] 就可以变为 (m * prime[j+1]) * prime[j],这说明 i * prime[j+1] 是 prime[j] 的整数倍,不需要再进行标记 (在之后会被 prime[j] * 某个数 标记)
对于 prime[j+2] 及之后的素数同理,直接跳出循环,这样就避免了重复标记。