1. 原理:
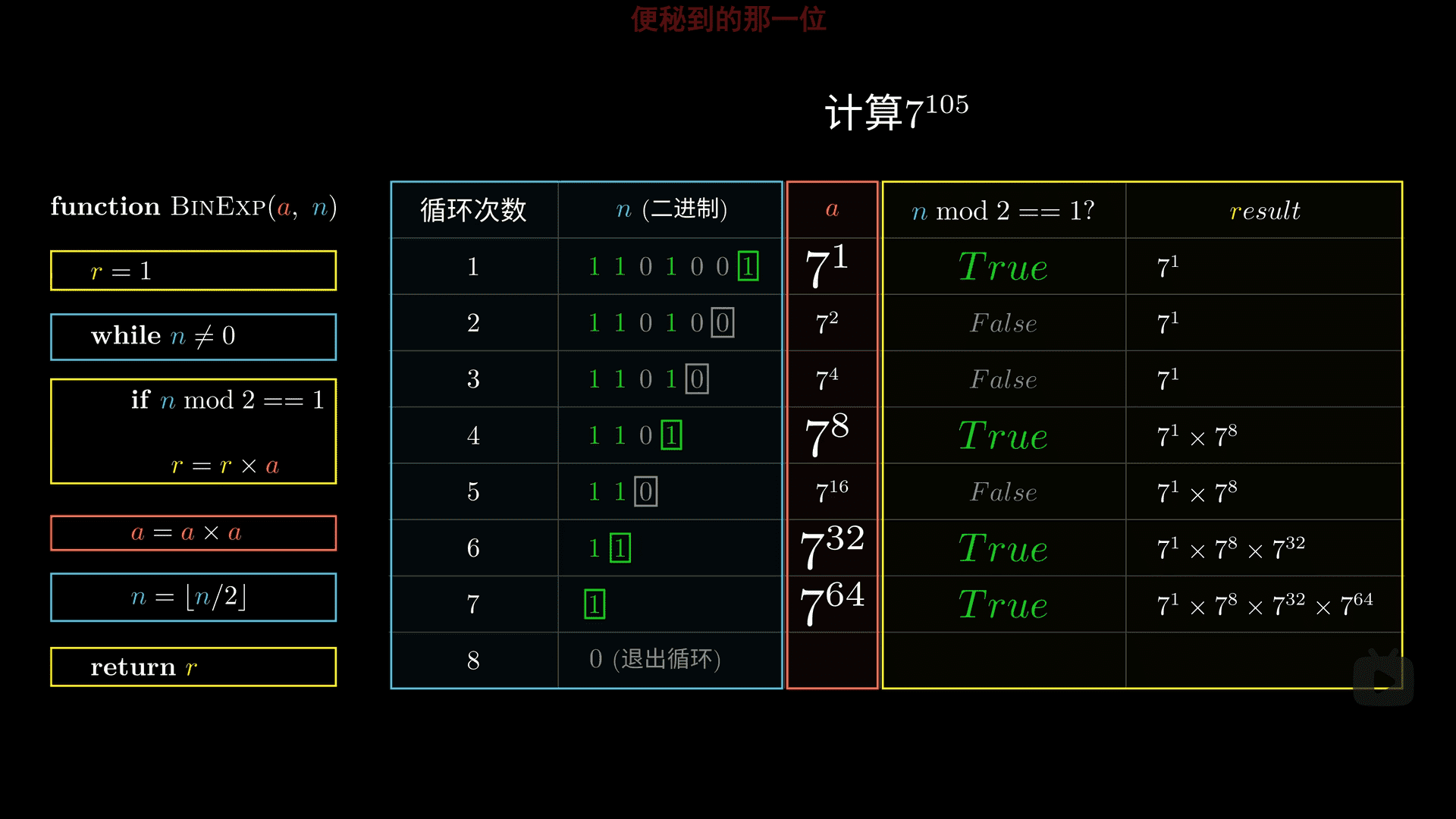
如图,任意一个正整数都可以表示成数个2的n次方之和。所以如a^105 = a*(a^8)(a^32)(a^64) 
而a^(2^n)运算可以利用a^(2^n/2)的运算结果,总之a^(2^n)运算量非常小。
从而可以快速的对所求数进行幂运算
2. 伪代码:
function BINEXP(a, n) r = 1 //初始化 while n!=0 if n & 1 == 1 //取遍历数2^n二进制最后一位判断。&为按位与运算。 r = r * a //乘上所有拆分项计算结果 a = a * a //配合n的遍历次数来计算a^(2^n) n = n>>1//遍历2的2到n次方 return r
3. C语言代码实现:
long long BINEXP(long long a, int n) {
long long r = 1;
for (; n != 0;) {
if (n & 1 == 1) {//取遍历数2^n二进制最后一位判断。&为按位与运算。
r = r * a;//乘上所有拆分项计算结果
}
a = a * a;//配合n的遍历次数来计算a^(2^n)
n = n >> 1;//遍历2的2到n次方
}
return r;
}注意,输出long long类型的格式符为%lld
4. C语言快速幂取模代码:
int BINEXP(int a, int n, int m) {
a = a % m; //初始化对第一个拆分项取模
int r = 1;
for (; n != 0;) {
if (n & 1 == 1) {//取遍历数2^n二进制最后一位判断。&为按位与运算。
r = (r * a) % m; //保证最后结果再取模
}
a = (a * a) % m; //对每个可能拆分项都取模
n = n >> 1;//遍历2的2到n次方
}
return r;
}