高数下八 5 空间曲面

本笔记为视频辅助笔记

1. 总结:

1. 曲面图像和方程的相互转换:

1.1. 实例:

对该方程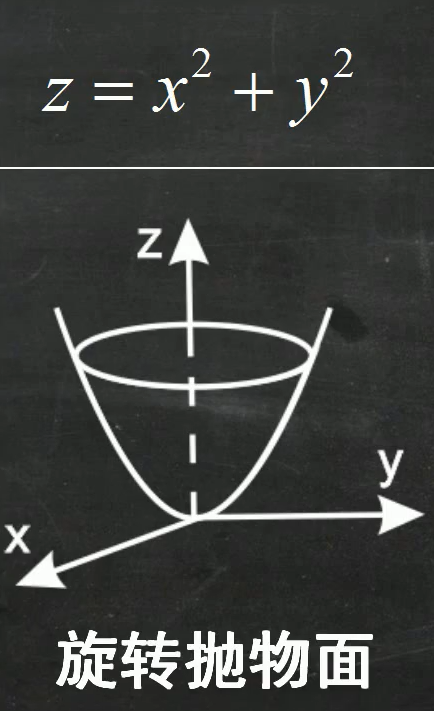

1. 已知z旋转轴
2. 原旋转平面可能有两个, 这里取xoz平面
3. 将y=0代入原方程, 得到旋转曲线方程为z=x²
4. 脑中想象z=x²沿着z转一圈

1.2. 先判断是不是旋转曲面(⭐)

1. 

1.1.1.1. 直观理解:

1. 没有根号的是旋转轴, 则旋转面原来的空间必须包含旋转轴
2. 根号下的两个未知数之中, 肯定有一个是旋转面原来空间所没有的
   1. 即是被旋转出来的

1.1.1.2. 解释:

有两组可能

1. 平面曲线为f(z,x) f(z,x)绕x轴旋转
   1. 把y=0代入曲面方程, 可得该结论
2. 平面曲线为f(y,x) f(y,x)绕x轴旋转
   1. 把z=0代入曲面方程, 可得该结论

1.3. 再用截痕法判断(⭐):

1. 分别在以下三个平面切, 得到截痕
   1. 垂直z轴, (代入z=0)
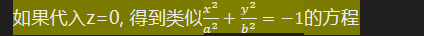      1. 把z取大一点,直到把-1变成正数
   2. 垂直y轴, (代入y=0)
   3. 垂直x轴, (代入x=0)
2. 然后根据这三个平面切出来的曲线来想象出曲面的轮廓

2. 求曲面在坐标面的投影：

1. 想象出曲面的图像
2. 投影到坐标面上时用不等式表示面

2. 旋转曲面：

1. 相关概念:

1.1. 母线：

用来旋转的一条曲线

2. 对所有旋转曲面的重要性质:

2.1. 绕特定坐标轴旋转的旋转曲面方程的规律：

先假设曲线在坐标轴平面内(从特殊入手)

如在xoy平面的曲线方程为 f(x,y) 则只能绕x轴或y轴旋转 最终的曲面方程中x,y,z三个未知数都有

2.2.1.1. 直观理解:

1. 绕x轴转的话, 原曲线的每一点x坐标都没有改变
2. 而另一个坐标的值就是点到旋转坐标轴的距离, 相当于半径
   1. 当曲线转出平面之后, 点到旋转坐标轴的距离就变成了根号平方和

3. 一些较特殊的旋转面:

3.1. 旋转双曲面:

2.3.1.1. 旋转单叶双曲面:

2.3.1.1.1. 方程:

2.3.1.2. 旋转双叶双曲面:

2.3.1.2.1. 方程:

4. 对其他旋转曲面:

1. 先写出某个在坐标轴平面上的曲线
2. 然后套用旋转曲面的一般方法进行处理

3. 球面:

1. 方程:

或

4. 基本的二次曲面:

1. 视频讲解:

《高等数学》同济版 全程教学视频（宋浩老师）_哔哩哔哩_bilibili

2. 相关概念:

2.1. 截痕:

用一个平面来截这个曲面, 得到的曲线像痕一样

2.2. 伸缩:

原图像 在x轴伸缩2倍, 即把$y=\frac{y}{2}$代入到原方程中

3. 椭圆锥面:

3.1. 梗概:

从这个曲面上面看, 截痕就是一个椭圆

3.2. 方程:

3.3. 直观理解:

1. 曲面就是曲线的集合
2. 当z=0时
3. 当z为变量的时候就是无数多条曲线
   1. 合起来就是一个椭圆曲面

4. 椭球面:

4.1. 方程:

4.2. 直观理解:

从三个平面切都是椭圆

4.3. 由平面椭圆变化到椭球面的过程:

(https://b23.tv/McCQuME)

5. 抛物面:

5.1. 椭圆抛物面:

4.5.1.1. 方程:

4.5.1.2. 直观理解:

1. 垂直于z轴切是椭圆
2. 垂直于x轴和y轴都是抛物线

4.5.1.3. 椭圆抛物面与椭圆锥面的对比:

(https://b23.tv/GLtYPm7)

5.2. 双曲抛物面(马鞍面):

4.5.2.1. 方程:

4.5.2.2. 直观理解:

1. 垂直于z轴切是双曲线
2. 垂直于x和y轴切是方向相反的抛物线

5. 柱面:

1. 相关概念：

1.1. 准线：

柱面的垂直截痕为准线

1.2. 母线：

柱面的高为母线

2. 视频讲解:

《高等数学》同济版 全程教学视频（宋浩老师）_哔哩哔哩_bilibili

3. 梗概:

把准线延母线平移就得到了柱面