做题经验:
1. 计算∫dx∫dy格式的二重积分:
child::
计算∫dx∫dy格式的二重积分
实例:
指向原始笔记的链接
1. 相关概念:
1. 定积分结果:
定积分对谁求积分,计算结果会消去这个变量
2. 多元函数的积分:
类似多元函数的偏导数, 把于积分变量无关的当成常数
2. 计算梗概:
- 把二重积分转换为两层嵌套的一重积分, 被积函数不变, 但移动到内层积分中
- 把体积微分成一个个横截面,对横截面定积分为体积,此为外层积分
- 对微分横截面,用定积分求其面积,此为内层积分
1. 选取横截面有两种方向:
- 第一层积分,微分横截面为yoz; 第二层积分, 求横截面积时往x轴积分
- 第一层积分,微分横截面为xoz; 第二层积分, 求横截面积时往y轴积分
2. 选择横截面方向方法:
- 根据积分区域图形
- 像这种用x横截,可以把积分区域分成简单曲线包围的 ,就用x轴方向来截横截面
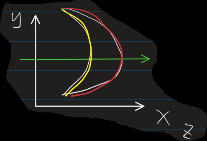
- 像这种用x横截,可以把积分区域分成简单曲线包围的 ,就用x轴方向来截横截面
- 根据解定积分计算的难易程度
2.1. 图示:
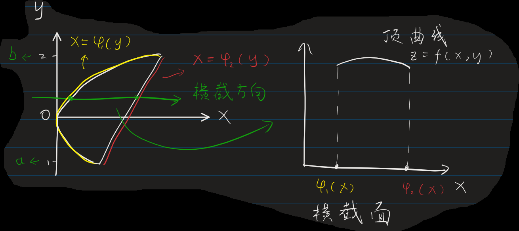 对应公式
对应公式![]()
5. 计算步骤:
- 在xoy平面内画出积分区域(俯视图)
- 往计算简单的方向进行积分(这里以先x后y为例)
- 确定内层积分:
上下限: 分别以横截方向(x)的上下曲线函数为上下限
微分元: 横截方向(dx)
- 注意: 需要把横截方向(x)为因变量
- 确定外层积分: 上下限: 垂直横截方向(y)的上下限 微分元: 垂直横截方向(dy)
- 把外层积分的未知数移动到内层积分
- 计算定积分:求不定积分流程归纳
6. 计算公式:
![]()
1. 为方便书写,也记作:
![]() 但是并不表示相乘
但是并不表示相乘
